티스토리 뷰
Lesson3. TapeEquilibrium
안녕하세요!
오랜만에 코딜리티 풀이를 하게 되었습니다. (너무 게을러서 흑...)
저번 시간에는 Lesson3. PermMissingElem에 대해 풀이해봤습니다.
이번에는 Lesson3의 마지막 문제인 TapeEquilibrium를 풀이해보려 합니다.
Question
https://app.codility.com/programmers/lessons/3-time_complexity/tape_equilibrium/
TapeEquilibrium coding task - Learn to Code - Codility
app.codility.com
N개의 정수로 구성된 비어있지 않은 배열 A가 주어지는데, 이를 평형(?)하게 만들어 차이를 구하여 가장 작은 값을 구하면 됩니다.
이해가 잘 안 되실 텐데요.. 아래 예제를 보시면 될 것 같습니다!
만약 배열 A: [1, 2, 3, 4, 5]가 주어졌을 때 다음과 같이 네 부분으로 나눌 수 있습니다.
1. [1], [2, 3, 4, 5]
2. [1, 2], [3, 4, 5]
3. [1, 2, 3], [4, 5]
4, [1, 2, 3, 4], [5]
이 네 부분은 콤마를 기준으로 했을 때 왼쪽과 오른쪽 배열로 나눠지며, 각 요소들의 합은
1. 1 - 14
2. 3 - 12
3. 6 - 9
4. 10 - 5
로 나타낼 수 있으며, 우리는 이 두 수들의 차를 구하여 절댓값이 가장 작은 값을 반환하면 됩니다.
1. -13 => 13
2. -9 => 9
3. -3 => 3
4. 5
이 예제에서는 3을 반환하면 되겠네요!
Answer
위의 예제에서, 배열을 두 부분으로 나눠 각 요소들의 합을 구했었습니다.
합을 구하는 특징을 보면, 인덱스가 증가 혹은 감소함에 따라 그 전에 더했던 값을 누적시키는 것을 볼 수 있는데요?
(예시. 왼쪽 배열: idx가 0일 경우 - A[0], idx가 1일 경우 - A[0] + A[1])
이 특징을 가장 잘 나타내는 메서드인 Array.prototype.reduce를 활용하여 한 번 풀이해봤습니다.
1. A 배열의 0번째 인덱스 부터 끝에서 2번째 인덱스까지 돌며, leftArr에 원소들의 합 push (idx: 0 -> A.length - 2)
2. A 배열의 마지막 인덱스 부터 1번째 인덱스까지 돌며, rightArr에 원소들의 합 push (idx: A.length - 1 -> 1)
3. leftArr (= rightArr)의 길이만큼 루프를 돌며, *subtractionArr[idx] = Math.abs(leftArr[idx] + rightArr[A.length - 1 - idx])를 실행
4. subtractionArr에서 가장 작은 값을 찾아서 반환
*subtractionArr[idx] = Math.abs(leftArr[idx] + rightArr[A.length - 1 - idx])
: A가 [1, 2, 3, 4, 5]일 때, leftArr은 [1, 3, 6, 10]이 들어가게 되고, rightArr에는 [5, 9, 12, 14]가 담기게 됩니다.
실제 원소들의 뺄셈을 할 때, [1, 3, 6, 10] - [5, 9, 12, 14] 처럼 이어지는게 아니라 [1, 3, 6, 10] - [5, 9, 12, 14] 와 같이 이어져야 하므로, rightArr의 idx는 배열의 마지막 인덱스 부터 줄어들도록 코드를 구성하였습니다.
풀이 코드는 아래와 같습니다. ( 시간 복잡도는 O(N) )
function solution(A) {
const arrLeng = A.length;
const leftArr = [];
const rightArr = [];
A.reduce((curr, next, idx) => {
// 초기값을 설정해주지 않으면 idx는 0이 아닌 1부터 시작합니다.
// 가장 처음에는 A 배열의 첫 번째 요소를 leftArr에 넣어야 하므로 다음과 같이 조건을 세웠습니다.
if (idx - 1 === 0) {
leftArr.push(curr);
}
const value = curr + next;
if (idx !== arrLeng - 1) {
leftArr.push(value);
}
return value;
});
A.reduceRight((curr, next, idx) => {
if (idx + 1 === arrLeng - 1) {
rightArr.push(curr);
}
const value = curr + next;
if (idx !== 0) {
rightArr.push(value);
}
return value;
});
const seperatedArrLeng = leftArr.length; // OR. rightArr.length
const subtractionArr = new Array(seperatedArrLeng);
for (let idx = 0; idx < seperatedArrLeng; idx++) {
subtractionArr[idx] = Math.abs(leftArr[idx] - rightArr[seperatedArrLeng - 1 - idx]);
}
return Math.min(...subtractionArr);
}
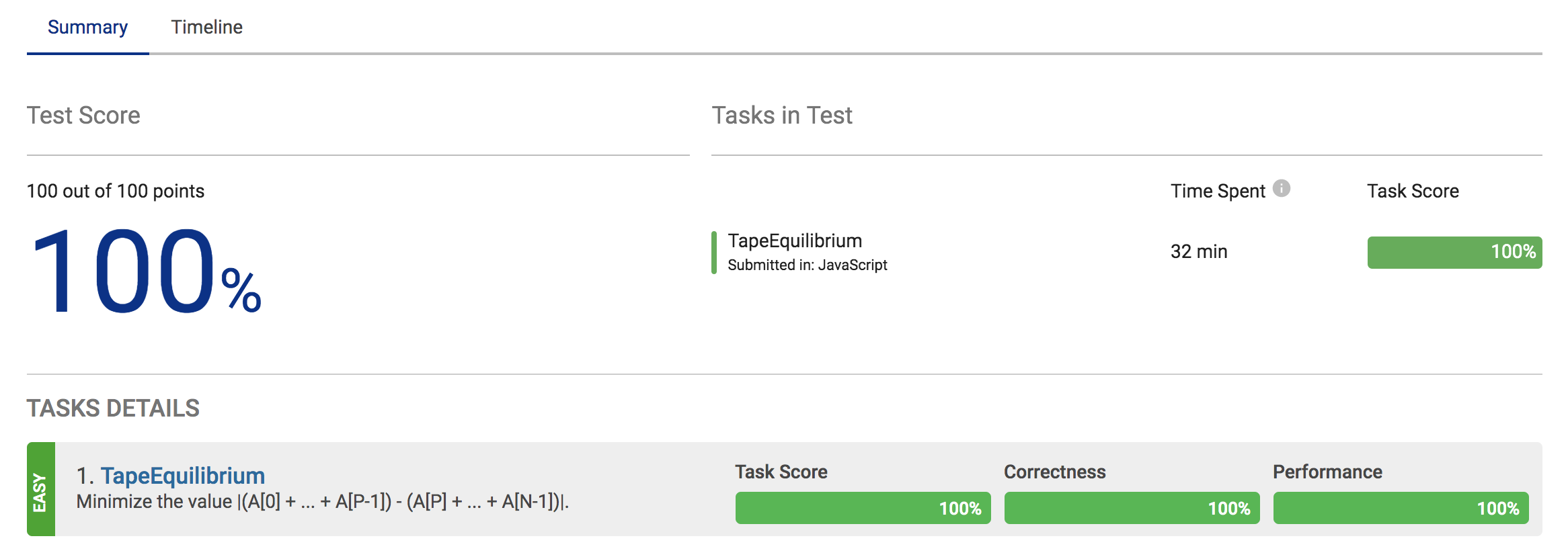
The End
너무 오랜만에 문제를 풀었던 것 같습니다.. lodash-own도 작업해야 하는데...
문제를 이해하고 난 후엔 비교적 쉽게 해결했는데, 좀 더 간단한 방법이 분명 있을 것 같다는 생각이 드네요.
좀 더 고민해봐야겠습니다!
지금까지 Lesson3의 마지막 문제인 TapeEquilibrium의 풀이였고,
다음 시간에는 Lesson4. PermCheck를 풀이해보려 합니다.
읽어주셔서 감사합니다!
'Codility' 카테고리의 다른 글
| Codility - FrogRiverOne 풀이 (0) | 2019.10.22 |
|---|---|
| Codility - PermCheck 풀이 (0) | 2019.06.23 |
| Codility - PermMissingElem 풀이 (0) | 2019.04.30 |
| Codility - FrogJmp 풀이 (0) | 2019.04.25 |
| Codility - OddOccurrencesInArray 풀이 (0) | 2019.04.23 |
- Total
- Today
- Yesterday
- react-waypoint
- 크롬 퍼포먼스 탭
- javascript
- dependencies
- react hoc 테스트
- infinite-scrolling 구현
- Package
- js debugger
- jest reducer test
- react-testing-library
- reducer test
- jest react test
- void 0
- axios
- react-infinite-scroll
- redux-mock-store
- devDependencies
- difference_1.default is not a function
- codility
- react-hooks test
- NPM
- esModuleInterop
- infinite-scrolling
- 효율적인 디버깅
- jest reducer 테스트
- hoc test
- vue.js
- tsconfig.json
- ES2020
- ES6 Module
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
